‍

float16的组成分为了三个部分：

  1. 最高位表示符号位；
  2. 有5位表示exponent位;
  3. 有10位表示fraction位;

FP16/BF16 在计算中的精度问题

1.4.1 溢出问题

  1. FP16 的可表示范围较 FP32 等更小，容易触发上、下溢出问题。

关于 FP16 的上下溢出可以参考图 1-3。对于绝对值大于 65504 的数，触发上溢出会舍入到±INF；对于绝对值小于的数，触发下溢出舍入到 0，具体示例可参考下表。

‍

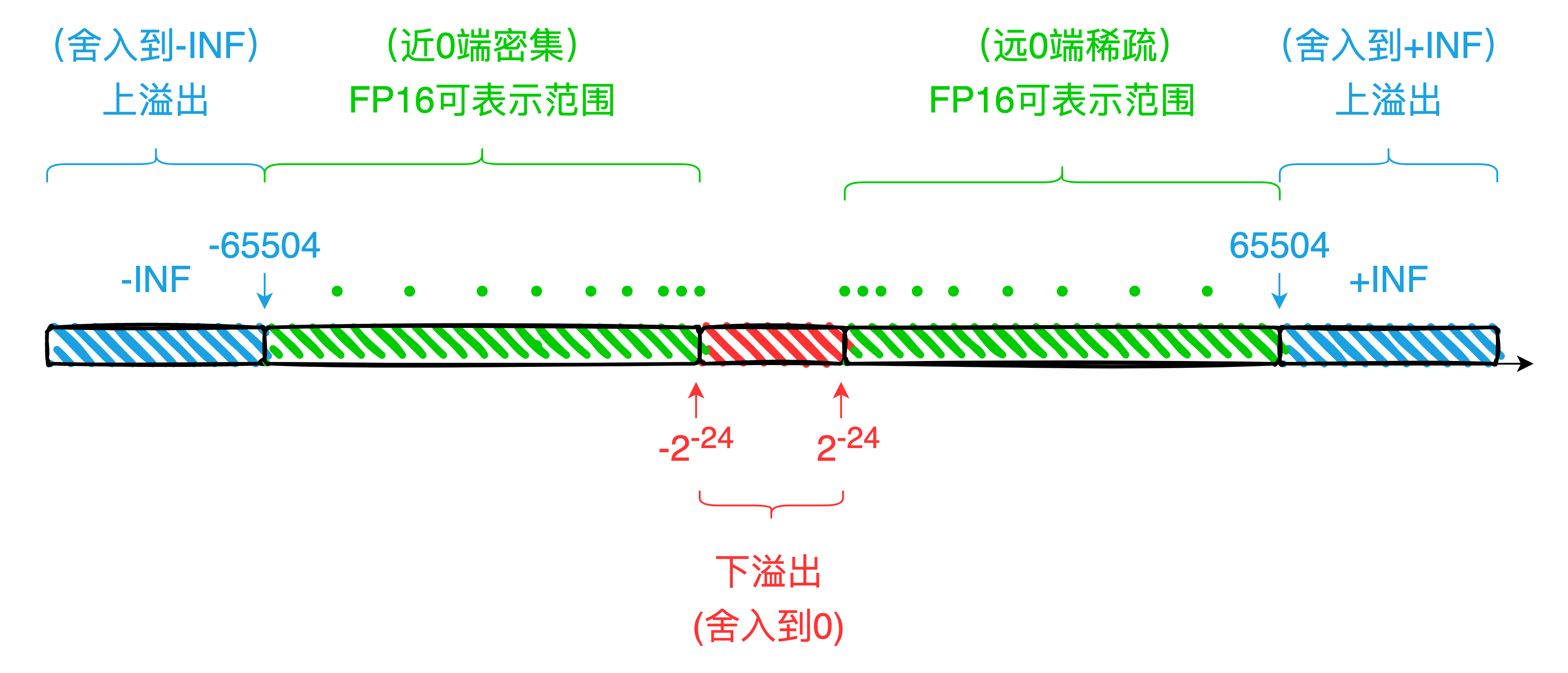
​../../_images/overflow.png

​

  1. BF16 则因为阶码同 FP32 等长，因此并不容易出现上下溢出问题。

1.4.2 舍入问题

  1. FP16 格式的浮点数最多只能表示 3 位有效数字，所以各浮点区间的固定间隔都是 Interval=Min∗2−10Interval=Min∗2^{−10}，也就是区间最小值的1/1024。

    1. 因此当 累加值加数>211\frac{累加值}{加数}>211 时，计算结果超过了 3 位有效数字；这会造成累加值最终无法被有效表示，累加结果会被舍入到累加值本身。

      1. 数值:1+0.0001=1.0001
      2. FP16: 1+0.0001=1.0001

    2. FP32 格式拥有 7 位有效数字的表达效果，因此当 FP32 格式向 FP16 格式转化时，也会出现精度的舍入问题。

      1. FP32：0.1234567
      2. FP16：0.1235

  2. BF16 格式的浮点数，在各个区间内的固定间隔是 Interval=Min∗2−7Interval=Min*2^{-7}​ ，故 BF16 相较于 FP16 的精度更低，也更容易出现 FP16 中所阐述的计算舍入和转换精度丢失的问题。

‍

下表摘自 wikipedia fp16，表示fp16不同区间的间隔，可见fp16的加法如果直接往param上加，会有很多失效。

Precision limitations

Min Max interval
0 2−13 2−24
2−13 2−12 2−23
2−12 2−11 2−22
2−11 2−10 2−21
2−10 2−9 2−20
2−9 2−8 2−19
2−8 2−7 2−18
2−7 2−6 2−17
2−6 2−5 2−16
2−5 2−4 2−15
2−4 ⁠1/8⁠ 2−14
⁠1/8⁠ ⁠1/4⁠ 2−13
⁠1/4⁠ ⁠1/2⁠ 2−12
⁠1/2⁠ 1 2−11
1 2 2−10
2 4 2−9
4 8 2−8
8 16 2−7
16 32 2−6
32 64 2−5
64 128 2−4
128 256 ⁠1/8⁠
256 512 ⁠1/4⁠
512 1024 ⁠1/2⁠
1024 2048 1
2048 4096 2
4096 8192 4
8192 16384 8
16384 32768 16
32768 65520 32
65520 ∞ ∞

‍

解决方法

溢出问题

损失放大（Loss Scaling） 即使用了混合精度训练，还是会存在无法收敛的情况，原因是激活梯度的值太小，造成了下溢出（Underflow）。损失放大的思路是：

  1. 反向传播前，将损失变化（dLoss）手动增大 2k2^k 倍，因此反向传播时得到的中间变量（激活函数梯度）则不会溢出；
  2. 反向传播后，将权重梯度缩 2k2^k 倍，恢复正常值。

‍

混合精度训练并不意味着所有的模型参数都用fp16训练，例如做layernorm、batchnorm时的参数一般就保持fp32的形式，Loss也保持fp32的形式，主要原因还是这些数值的精度对模型训练过程影响较大，同时它们占据的存储也不大，因此维持原始形式，越高精越好。

loss scale 有两种方式

  • 常量损失放大
  • 动量损失放大

‍

上溢出可以通过 clip gradient 解决

‍

‍

‍

舍入误差

可以在参数更新时将 fp16 转成fp32，weights, activations, gradients 等数据在训练中都利用FP16来存储，同时拷贝一份FP32的weights，用于更新。 参考论文：MIXED PRECISION TRAINING

‍

‍

参考资料：

【PyTorch】唯快不破：基于Apex的混合精度加速

paddle低精度算子支持开发规范

浅谈混合精度训练

‍